Ever since the discovery of a numerical representation of paint wear (aka. "Float Values") on Reddit back in 2015, they have redefined how the community prices skins and spawned a full collector niche.
But what exactly are float values and how do they work? How are they generated? How does this influence the probability of getting a low float skin?
The Representation of Wear
As you might expect, CS:GO skins have a dynamic system for computing the texture of each item. When Valve originally designed this, one of their goals was to make skins as unique as possible. As a result, one of those "unique" parameters is how much grunge and wear you see on the skin.
When an item is first created, the CS:GO Game Coordinator sets out the task of generating a random number between the minimum and maximum "float" range for that skin. This number is then used to determine the opacity of the grunge wear texture when the skin is displayed.
By default, if the skin creator has not overridden the range, it tries to generate within 0.06-0.80. You can find more details on this process and distribution on Analysis of Float Value and Paint Seed Distribution.
The closer to 1, the higher the opacity of the wear texture and more wear is shown on the texture.
What Exactly is a Float Value?
Computers represent numbers in binary arithmetic. Representing whole integers such as 1, 2, 3, 4 can be pretty trivial by mapping it to binary bits. For example, the right-most bit represents 1, next one is 2, then 4, etc...
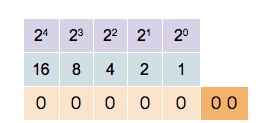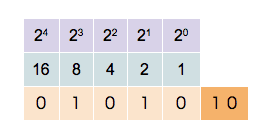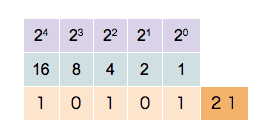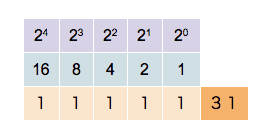
But how would we represent a number such as 0.0000123456 in this type of binary system? In this case, we'd define a float value as a number with arbitrary decimal precision.
For humans, this seems easy given that we can rewrite any arbitrary infinite precision decimal number into scientific notation. For example, 0.0000123456 could turn into 1.23456 x 10^-5. But what about a computer?
IEEE-754, A Standardized Format
As you might expect, there is a standardized format to represent float values called IEEE-754. This format allows us to represent numbers with varying levels of precision given how many bits we allocate to the format.

As we can see above, certain sections of the bit ranges are served for the sign, exponent, and fraction.
To break it down:
Sign: Determines whether the number is negative or not
Exponent: Determines the multiplicative exponent similar to scientific notation. Since we work with binary, the base is 2 instead of 10 and becomes 2^(exp-127). This ranges from -126 to 127.
Significand: 23 explicit bits that allow storing the decimal digits, this leads to roughly 7 digits of precision in 32-bit format.
This all comes together to form this:
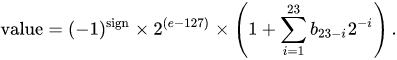
So what implications does this have?
Due to the reserved bits in the exponent, representing a number such as 0.00000003498433 is the same amount of space as 0.00000000000000000000000000000000003498433. This is because (in basic terms) the format can simply count how many zeroes it needs to put in the beginning or end.
Another result is that there is a limited amount of bits that can represent the "fractional" portion of the floating point. This is effectively the digits before or after the zeroes. In the 32-bit single precision IEE-754, this gives around 7 digits of precision. This means that we can represent roughly 7 digits after all the zeroes.
Not Really Infinite
While there are theoretically an infinite amount of floating point numbers between 0-1 or 0.0001-0.0002 or 0.000000001-0.000000002, there are only a finite numbers of bits (in this case 32-bits) to represent the float value within. As a result, there are actually a finite number of roughly 1 billion float values that exist within the 0-1 range.
Almost every float value (>0.001) that can exist within 0-1 has a weapon that corresponds to it
You can see this quite easily by looking at the amount of duplicate floats in any given range on FloatDB. Here's an example.
From there, you can also see how 0.34857350587845 jumps straight to 0.34857353568077 (a difference of 0.00000002980232). This just so happens to be after the cut off of roughly 7 digits of precision since you'll simply get an approximation when a value with more precision is encoded.
As a result, it is actually decently probable to get duplicate float values for two unique guns within CS:GO, even the top 4 highest floats in the game are duplicates (but are separate items).
Exponent Woes and Uniform Distributions
While being able to represent seemingly infinite precision is pretty cool, it makes our lives a bit more difficult when we try to generate a number between 0-1 with a uniform distribution.
What this means is that, if we generate a number between 0-1, each number should be equally probable to be picked. The problem is that there are many more representable float values between 0 and 0.0001 due to the exponent explained above. Float values are distributed logarithmically, not uniformly.
In fact, over 75% of float values between 0-1 exist within the 0-0.0001 range.
This is a problem, since if we just naively generate a random float between 0-1 it has a 75% of being between 0 and 0.0001. That's not uniform!
How CS:GO Uniformly Generates Floats
Valve has built a very large code base on the Source engine, which includes utilities for generating random numbers (turns out games like to incorporate randomness, who woulda known).
One of these is a Uniform Random generator in the Source SDK capable of generating random floats and integers distributed uniformly within given ranges.
Due to my previous attempts in reverse engineering how skins work, I ported this random generator into Golang here. We're able to independently verify that this is in-fact the same generator used to create float values on Valve's servers (aka. Game Coordinator).
But how does this generator fix the uniform distribution problem with floats?
Well, it turns out there's a pretty simple answer. What the game does is effectively try to generate a random integer within 0-2147483647 (max signed 32-bit integer) and simply divides the result by 2147483647.
This allows us to effectively generate 2147483647 unique floats between 0-1, uniformly distributed. But remember how there are only around a billion floats that can actually be represented in IEEE-754 within 0-1? Well, the system then tries to find the closest IEEE-754 to the random number it picked, which is then chosen as the approximation. In real terms, this cuts the amount of representable float values down around 10 fold.
Probability of Very Low/High Floats
It turns out that we can figure out what the lowest float skin in the game can actually be. Currently, it is the 0.00000000089966 M249 | Gator Mesh.
If we take 0.00000000089966 * 2147483647, we find that it likely originally generated the number 3 out of 2147483647 (when taking into account the float range).
If we run Monte Carlo simulations, the odds of getting the new lowest float skin with a skin in the range of 0-1 is roughly 1 in a billion.
The lowest possible float is heavily dependent on max float range since it is effectively a multiplier. The M4A1-S | Hot Rod has one of the lowest max floats of only 0.08 and likely one of the lowest in the game. This would give us a lowest possible float at 0.08 * 1 / 2147483647 = 0.00000000003725.
In terms of the highest float in the game, unfortunately there is a cap hard-coded with a max of 1-1.2e-7, which is what you see as the highest float in the game on FloatDB.
Final Thoughts
It turns out that it is much harder to hit the lowest possible float value than to hit the highest (which has already been done 4 times!). Float values are approximations and due to their finite nature, we can find duplicate floats at almost every wear range.
If you'd like to learn more, check out our blog post on the distribution of float values and paint seeds.
Want to join our community? Follow us on Twitter or join our Discord and Steam Group.